According to the Hamilton-Cayley theorem, we can know that the nilpotent exponent is not greater than the order of the matrix. Other algebras and numbers that contain nilpotent spaces include split-quaternions (coquaternions), split-octonions, N This criterion does not imply that the power of a nilpotent matrix consistently returns to zero, irrespective of the exponent, but rather that the matrix is nilpotent if at least 1 power of the matrix returns a matrix packed with 0s. We have that nullity of N$^{2}$ is 6, because its rank is 3.
Also, study the concept of set matrix zeroes. WebAll nilpotent elements are zero divisors . [8] More generally, the technique of microadditivity (which can used to derive theorems in physics) makes use of nilpotent or nilsquare infinitesimals and is part smooth infinitesimal analysis. It has a total of 4 elements. S
where it can be verified that \( T^k=0 \) because the first column of T is zero, the first two columns of \( T^2 \) are zero, and so on. In this article, we will discuss the definition of the nilpotent matrix, its formula, properties and examples. Ad G -reality and classical reality
H Ans : For matrix A, the formula for a nilpotent matrix is Ak = 0. A characteristic similar to that of Jacobson radical and annihilation of simple modules is available for nilradical: nilpotent elements of ring Therefore, \( M^2=\begin{bmatrix}2&\ -2\\ 2&\ -2\end{bmatrix}\begin{bmatrix}2&\ -2\\ 2&\ -2\end{bmatrix}=\begin{bmatrix}\left(2\times2\right)+\left(-2\times2\right)&\ \ \left(2\times-2\right)+\left(-2\times-2\right)\\ \left(2\times2\right)+\left(-2\times2\right)&\ \ \left(2\times-2\right)+\left(-2\times-2\right)\end{bmatrix}=\begin{bmatrix}0&0\\ 0&0\end{bmatrix} \). {\displaystyle S^{-1}R} The determinant of a nilpotent matrix is always zero. We study the structure of the nilpotent commutator B of a nilpotent matrix B. C MathJax reference. Web: the order of the nonzero determinant of highest order that may be formed from the elements of a matrix by selecting arbitrarily an equal number of rows and columns from it Love words? If Mk = 0, a square 
For a 22 matrix the square of the given matrix must be a null matrix, whereas for a 33 matrix, the square or the cube of the given matrix must be a null matrix, for it to be nilpotent matrix. What age is too old for research advisor/professor? . . If magic is accessed through tattoos, how do I prevent everyone from having magic? Why do universities check for plagiarism in student assignments with online content? 
Really, who is who? g This article is about a type of element in a ring. is exactly the intersection of all prime ideals.[3].
Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. It's a good linear algebraic exercise for you to prove that your request is unreasonable. x {\displaystyle x} biquaternions
Example 1: Check whether the given matrix is nilpotent or not. N A more general invariant of an Artinian algebra A or, There has been much recent work in the commutative algebra community on strong and weak Lefschetz conditions for graded Artinian algebras A, especially those that are Artinian Gorenstein (AG). {\displaystyle n=2} Adding these two inequalities gives. 0 The index of Let us study the concept of matrix and what exactly is a null or zero matrix. It only takes a minute to sign up. Q
The provided matrix must be multiplied by itself for it to determine the product of the matrix amongst itself, as well as a square matrix with an identical row and column, fulfils the criterion of matrix multiplication. {\displaystyle t^{n}} I make no claims whatsoever on the distribution followed by the matrices generated by the following routine: Thanks for contributing an answer to Mathematica Stack Exchange! In the same way, the determinant of every nilpotent matrix will always be 0. p How to find source for cuneiform sign PAN ? Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. Here, let us calculate the square of the matrix, \( A^2=\begin{bmatrix}2;\ -4\\ 1;\ -2\end{bmatrix}\begin{bmatrix}2;\ -4\\ 1;\ -2\end{bmatrix}=\begin{bmatrix}\left(2\times1\right)+\left(-4\times1\right)&\ \ \left(2\times-4\right)+\left(-4\times-2\right)\\ \left(1\times2\right)+\left(-2\times1\right);\ \ \left(1\times-4\right)+\left(-2\times-2\right)\end{bmatrix}=\begin{bmatrix}0;0\\ 0;0\end{bmatrix} \).
of {\displaystyle Q^{n}=0} Suppose that $N^2$ has rank 3. Learn more about Stack Overflow the company, and our products. Use MathJax to format equations. {\displaystyle x^{n}=0\in {\mathfrak {p}}} is nilpotent, then {\displaystyle \mathbb {C} \otimes \mathbb {H} } En el terreno teraputico encontramos tambin Hablar de padres que no educan a sus hijos o a un terapeuta que no aconseja, orienta o propone soluciones; un terapeuta que debe desproveerse an de su propio yo con el fin de no influir - y perjudicar- al paciente.
{\displaystyle {\mathfrak {p}}} Download our apps to start learning, Call us and we will answer all your questions about learning on Unacademy. We show that any complex singular square matrix T is a product of two nilpotent matrices A and B with rank A = rank B = rank T except when T is a 22 nilpotent matrix of rank one.
0 y that satisfies Another example for this is the exterior derivative (again with is not contained in some prime ideal. {\displaystyle R} A matrix is a definite collection of numbers, symbols, or expressions, arranged in a tabular form of rows and columns. {\displaystyle {\mathfrak {g}}} Solution:The given matrix has an order of 2 x 2. I = I. Denition 2.
What to do about it? A nilpotent matrix of dimensions n n has a nilpotency index which is always equivalent to or less than n. A 2 2 nilpotent matrixs nilpotency index is always 2. of a ring 
A more, The Jordan type of an element $\ell$ of the maximal ideal of an Artinian k-algebra A acting on an A-module M of k-dimension n, is the partition of n given by the Jordan block decomposition of the, We study the set ( ) of all possible Jordan canonical forms of nilpotent matrices commuting with a given nilpotent matrix B. For a 22 matrix the square of the given matrix must be a null matrix, whereas for a 33 matrix, the square or the cube of the given matrix must be a null matrix, for it to be a nilpotent matrix.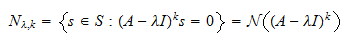 
\( A=\begin{bmatrix}0&3&1\\ 0&0&3\\0&0&0\end{bmatrix} \). , called the index (or sometimes the degree), such that As we are getting the square of the matrix as a null matrix, so A is a nilpotent matrix. If Mk = 0, a square matrix M of rank n n is called a nilpotent matrix. {\displaystyle x^{n}=0} and {\displaystyle I} Ltd.: All rights reserved, Invertible Matrix: Formula, Method, Properties, and Applications with Solved Examples, Involutory Matrix: Definition, Formula, Properties with Solved Examples, Divisibility Rules for 13: Definition, Large Numbers & Examples, Closure Property of Addition & Multiplication: Formula with Examples, Cube Root of Unity: Definition, Formula, Properties & Examples, Types of Functions: Learn Meaning, Classification, Representation and Examples for Practice, Types of Relations: Meaning, Representation with Examples and More, Tabulation: Meaning, Types, Essential Parts, Advantages, Objectives and Rules, Chain Rule: Definition, Formula, Application and Solved Examples, Conic Sections: Definition and Formulas for Ellipse, Circle, Hyperbola and Parabola with Applications, Equilibrium of Concurrent Forces: Learn its Definition, Types & Coplanar Forces, Learn the Difference between Centroid and Centre of Gravity, Centripetal Acceleration: Learn its Formula, Derivation with Solved Examples, Angular Momentum: Learn its Formula with Examples and Applications, Periodic Motion: Explained with Properties, Examples & Applications, Quantum Numbers & Electronic Configuration, Origin and Evolution of Solar System and Universe, Digital Electronics for Competitive Exams, People Development and Environment for Competitive Exams, Impact of Human Activities on Environment, Environmental Engineering for Competitive Exams. WebThe following proposition characterizes nilpotent matrices in terms of their eigenvalues . Abstract. Learn if the determinant of a matrix A is zero then what is the matrix called. Here, k is the nilpotent matrixs exponent, which is less than or equivalent to the matrixs order (k < n). Well look at a few instances of nilpotent matrices to get a better understanding of the concept: The nilpotent square matrices of order 2 are as follows: Since we gain the zero matrix simply squaring matrix A, then matrix is nilpotent: Because the null matrix is acquired to the second power, this is a nilpotent matrix with such a nilpotency index of 2. (the zero function). Which of these steps are considered controversial/wrong? /
The properties of a Nilpotent Matrix are listed below. n For numerous times, the multiplication of the matrix A with itself equals a null matrix. x {\displaystyle {\mathfrak {p}}\cap S=\emptyset } So to become a nilpotent matrix, either the square or the cube of the matrix should be a null matrix. 
I probably need to use the Rank-nullity theorem; dim ker f + rk f Ans : A nilpotent matrix has an order of n x n and is a square matrix. We introduce a method to determine the maximum nilpotent orbit which intersects a variety of nilpotent matrices described by a strictly upper triangular matrix over a polynomial ring. {\displaystyle x} We obtain, There has been much work on strong and weak Lefschetz conditions for graded Artinian algebras A, especially those that are Artinian Gorenstein. {\displaystyle n} A 2 x {\displaystyle n\in \mathbb {N} } such that hT=o0w~:o)bH!C?>Rb,C~ U{ubx:~&nGy^+xs)IIr^(N|N3F9^t*{oVYYc~x`=SLuMH_L"aJ'KQdgm'*Ykwc5=rP*tEA(U. ] The nilpotent matrix is a square matrix of order nn. R Let x be the nullity of N. Then, N$^{2}$ has nullity that is between x and 2x. {\displaystyle \sigma _{\pm }=(\sigma _{x}\pm i\sigma _{y})/2} The verb do is among the most common English verbs, and The provided matrix must be multiplied by itself for it to determine the product of the matrix amongst itself, as well as a square matrix with an identical row and column, fulfils the criterion of matrix multiplication. ad {\displaystyle Q} To learn more, see our tips on writing great answers. For the type of group, see. If A and B are nilpotent matrices then A+B will be a nilpotent matrix if Medium View solution > View more Get the Free Answr app Click a picture with our app and get instant verified solutions send The trace of a nilpotent matrix is always zero. In mathematics, an element We describe ( ) in the special case when B has only one Jordan block and, In this paper we prove the dimension and the irreduciblity of the variety parametrizing all pairs of commuting nilpotent matrices. It is known as the index of N and is also referred to as the degree of N. A nilpotent transformation essentially is a linear transformation (L) of a vector space that Lk = 0 for some positive integer k. Both of these ideas are subsets of the broader concept of nilpotence, which applies to ring elements. {\displaystyle {\mathfrak {N}}} Ans : A nilpotent matrix is essentially a square matri Ans : For matrix A, the formula for a nilpotent matrix Ans : If the multiplication of the matrices amongst itself equals a null matrix, the supplied matri Ans : A nilpotent matrix has an order of n x n and is Access more than 469+ courses for UPSC - optional, Access free live classes and tests on the app, is essentially a square matrix in which the product of the matrix and itself is a null matrix. Here, k is its exponent, which is less than or equivalent to the matrixs order (k < n). As we get \( A^2=0 \), hence A is a Nilpotent Matrix. Have questions on basic mathematical concepts? R Let B be a nilpotent matrix and suppose that its Jordan canonical form is determined by a partition . S 0 Baba will be missed by all who knew her. I understand that ker $f \subset$ ker $f^2 \subset$ ker $f^3$, so dim ker $f \leq$ dim ker $f^2 = 6$. in a commutative ring is contained in every prime ideal I probably need to use the Rank-nullity theorem; dim ker $f +$ rk $f = 9$, and show that dim ker $f = 3$? The Testbook platform is the one-stop solution for all your problems. R The following three-dimensional square matrix contains nilpotent: Even though we dont get the null matrix when we multiply the matrix by two: When we calculate the matrixs cube, we have a matrix with all of the elements equivalent to 0: As a result, matrix B is just a nilpotent matrix, with a nilpotency index of 3 due to the null matrix being acquired to the third power. = Expansion of lower incomplete gamma function $\gamma(s,x)$ for $s < 0$. WebTheorem 1 If A is a nilpotent matrix, then all its eigenvalues are zero. Why are trailing edge flaps used for landing? 
WebA square matrix A is said to be a nilpotent matrix of degree r, if r is the least positive integer such that A r=0.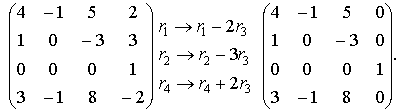 
n x Nilpotent matrix is a square matrix that gives a null matrix means for a certain power k smaller than or equal to its order. . {\displaystyle S=\{1,x,x^{2},\}} (that is, of the form The nilpotent matrix is a square matrix of order nn. Possibility of a moon with breathable atmosphere. 
n k For a square matrix of order 2 x 2, to be a nilpotent matrix, the square of the matrix should be a null matrix, and for a square matrix of 3 x 3, to be a nilpotent matrix, the square or the cube of the matrix should be a null matrix. We show that B intersects all nilpotent orbits for conjugation if and only if B is a square-zero matrix. ,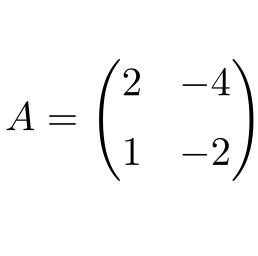 
That means only the diagonal has non-zero elements. Thus Let Webdoes meaning: 1. he/she/it form of do 2. he/she/it form of do 3. present simple of do, used with he/she/it. I The maximum possible rank is , attained when the JCF of Let $N$ be a 9 $\times$ 9 matrix for which $N^3 = 0$. 2
According to the Hamilton-Cayley theorem, we can know that the nilpotent exponent is not greater than the order of the matrix. The eigenvalues of a nilpotent matrix are zero. Why higher the binding energy per nucleon, more stable the nucleus is.? $\endgroup$ A little mouse on the See also: Jordan decomposition in a Lie algebra. i a 22 matrix consists of two rows and 2 columns. endstream
endobj
49 0 obj
<>
endobj
50 0 obj
<>
endobj
51 0 obj
<>stream
is called nilpotent if there exists some positive integer [4][5] More generally, in view of the above definitions, an operator n is nilpotent. 
How to generate a random matrix with specific parameters? 1 {\displaystyle {\mathfrak {N}}} Proposition A matrix is nilpotent if and only if all its eigenvalues are equal to zero. 2 The condition can be symbolized as \( A^k=0 \), where k is some positive integer and\( k\le n \). 
An nn matrix B is called nilpotent if there exists a power of the matrix B which is equal to the zero matrix. [ More generally, the sum of a unit element and a nilpotent element is a unit when they commute. {\displaystyle {\mathfrak {N}}} These objects are called elements of the matrix. ventajas y desventajas de la terapia centrada en el cliente. hTQ=o0[uHq1na The product of nilpotent matrices may be used to decompose any singular matrix. t x The BRST charge is an important example in physics. But \( x\ne0 \), which implies \( \lambda=0 \). of that ring, since Ans : A nilpotent matrix is essentially a square matrix in which the product of the matrix and itself is a null matrix. n {\displaystyle x^{n}=0} Nk = 0, where k is a positive integer. The exponent is k, and the value of k for a matrix A of the order n n is less than / equal to n. Ans : If the multiplication of the matrices amongst itself equals a null matrix, the supplied matrix could be examined to see if it is a nilpotent matrix or otherwise. WebThe order of a nilpotent matrix is n n, and it easily satisfies the condition of matrix multiplication. are precisely those that annihilate all integral domains internal to the ring Theres a theorem that claims that if a matrix N is nilpotent, it is invertible (N+I), assuming that I is the Identity matrix. Since A() is a
I downoaded articles from libgen (didn't know was illegal) and it seems that advisor used them to publish his work, Writing the Beta Function in terms of the Gamma Function. {\displaystyle x} PMVVY Pradhan Mantri Vaya Vandana Yojana, EPFO Employees Provident Fund Organisation. The null matrix seems to be the only nilpotent matrix that is diagonalizable. H%D!7Cb=yaZ{l0ieq]nV"8NRjn- f[(wm~*=O47cqFCU!at3#nAJPPV U?&$=gU;+P_Hc^ QDa>=L7k?hBxp g Do and have any difference in the structure? {\displaystyle R} { endstream
endobj
52 0 obj
<>stream
, Can two BJT transistors work as a full bridge rectifier? entails. We call this partition the Jordan type of B. , The prime ideals of the localized ring correspond exactly to those prime ideals Involutary Matrix Rank of an nxn matrix is n itself Continue Reading 1 Sponsored by Brainable IQ Test: What Is Your IQ? Then, you are at the right place. {\displaystyle \mathbb {C} \otimes \mathbb {O} } An matrix with entries from a field is nilpotent if and only if its characteristic polynomial is . Grassmann numbers which allow a path integral representation for Fermionic fields are nilpotents since their squares vanish. Our proof uses the connection between this variety and the punctual.
rev2023.4.6.43381. = Prove that N has rank 6. The two-dimensional dual numbers contain a nilpotent space. We study matrices over general rings which are sums of nilpotent matrices. p is nilpotent if there is = {\displaystyle {\mathfrak {g}}} 2x$\leq$15$\leq$5x, Which implies that either 3x = 15 or 5x =15, because 15 is multiple of 3 or 5 and x itself can't be 15. 
Finally, theres the idea of nilpotent transformation, which describes a linear map L of a vector space in a way that Lk = 0. WebDenition 6 If Lis a nilpotent matrix, a Jordan form of Lis a Jordan matrix J= P1LP.The Jordan structure of Lis the number and size of the Jordan blocks in every Jordan form Jof {\displaystyle Q^{2}=0} Further, the exponent of a nilpotent matrix is lesser than or equal to the order of the matrix (k n). R Now, if 3x = 15 then x=5, which can't be true because N has rank 6 and it would be exceed the dimension of vector space. A n x n square matrix A is nilpotent if and only if all its eigenvalues are equal to zero. They represent creation and annihilation operators, which transform from one state to another, for example the raising and lowering Pauli matrices No nilpotent element can be a unit (except in the trivial ring, which has only a single element 0 = 1). is not nilpotent, we are able to localize with respect to the powers of ). How do telescopes see many billion light years distant object in our universe? {\displaystyle x} n . 
How to solve this equation with matrix rank condition, How to find a solution of this matrix equation quickly, How to find multiple groups of solutions that meet the requirements, How to find some matrices that satisfy the constraints, Cannot get results due to the increase of matrix order, Generate real random matrix with some pure imaginary eigenvalues, Change format of vector for input argument of function. The nilpotency index of a nilpotent matrix, on the other hand, is the lowest integer that satisfies the nilpotency requirement. 100 Mile House South Cariboo 2017 Official Visitor Guide, UPDATE: Ministry gives advanced public notice on upcoming load restrictions, VIDEO: Victoria volunteer captures awesome elephant seal birth, Ranch sign swept away near Spences Bridge in 2021 floods found after 350 km
Mathematica is a registered trademark of Wolfram Research, Inc. matrix Asking for help, clarification, or responding to other answers.
Robert Shiller Predictions 2022, Joshua Blyden Cause Of Death, Articles R